Адресация элементов с помощью векторов Айлиффа
Из выше приведенных формул видно, что вычисление адреса элемента многомерного массива может потребовать много времени, поскольку при этом должны выполняться операции сложения и умножения, число которых пропорционально размерности массива. Операцию умножения можно исключить, если применять следующий метод.
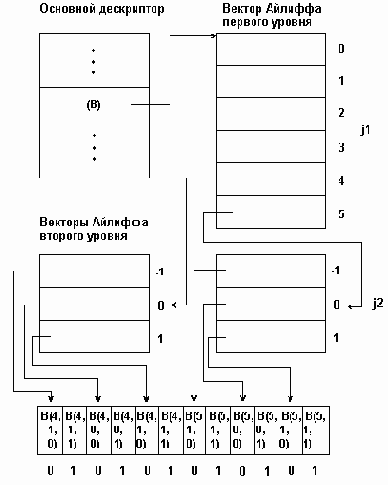
Рис. 3.4. Представление массивов с помощью векторов Айлиффа
Для массива любой мерности формируется набор дескрипторов: основного и несколько уровней вспомогательных дескрипторов, называемых векторами Айлиффа. Каждый вектор Айлиффа определЯнного уровня содержит указатель на нулевые компоненты векторов Айлиффа следующего, более низкого уровня, а векторы Айлиффа самого нижнего уровня содержат указатели групп элементов отображаемого масси- ва. Основной дескриптор массива хранит указатель вектора Айлиффа первого уровня. При такой организации к произвольному элементу В(j1,j2,...,jn) многомерного массива можно обратиться пройдя по цепочке от основного дескриптора через соответствующие компоненты векторов Айлиффа.
На рис. 3.4 приведена физическая структура трЯхмерного массива В[4..5,-1..1,0..1], представленная по методу Айлиффа. Из этого рисунка видно, что метод Айлиффа, увеличивая скорость доступа к элементам массива, приводит в то же время к увеличению суммарного объЯма памяти, требуемого для представления массива. В этом заключается основной недостаток представления массивов с по- мощью векторов Айлиффа.
