Бинарные деревья.
Существуют m-арные деревья, т.е. такие деревья у которых полустепень исхода каждой вершины меньше или равна m (где m может быть равно 0,1,2,3 и т.д.). Если полустепень исхода каждой вершины в точности равна либо m, либо нулю, то такое дерево называется ПОЛНЫМ m-АРНЫМ ДЕРЕВОМ.
При m=2 такие деревья называются соответственно БИНАРНЫМИ, или ПОЛНЫМИ БИНАРНЫМИ.
На рисунке 6.12(a) изображено бинарное дерево, 6.12(b)- полное бинарное дерево, а на 6.12(c) показаны все четыре возможных расположения сыновей некоторой вершины бинарного дерева.
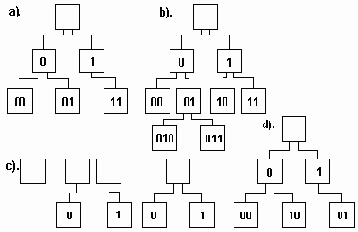
Рис. 6.13. Изображения бинарных деревьев
Бинарные деревья, изображенные на рис.6.13(a) и 6.13(d), представляют собой разные позиционные деревья, хотя они не являются разными упорядоченными деревьями.
В позиционном бинарном дереве каждая вершина представлена единственным образом посредством строки символов над алфавитом {0,1}, при этом корень характеризуется пустой строкой. Любой сын вершины "u" характеризуется строкой, префикс (начальная часть) которой является строкой, характеризующей "u".
Примером бинарного дерева является фамильное дерево с отцом и матерью человека в качестве его потомков. Еще один пример - это арифметическое выражение с двухместными операциями, где каждая операция представляет собой ветвящийся узел с операндами в качестве поддеревьев.
Представить m-арное дерево в памяти ЭВМ сложно, т.к. каждый элемент дерева должен содержать столько указателей, сколько ребер выходит из узла (при m-3,4.5.6... соответствует 3,4,5,6... указателей). Это приведет к повышенному расходу памяти ЭВМ, разнообразию исходных элементов и усложнит алгоритмы обработки дерева. Поэтому m-арные деревья, лес необходимо привести к бинарным для экономии памяти и упрощению алгоритмов. Все узлы бинарного дерева представляются в памяти ЭВМ однотипными элементами с двумя указателями (см.разд. 6,2,5), кроме того, операции над двоичными деревьями выполняются просто и эффективно.
