Целые типы

С помощью целых чисел может быть представлено количество объектов, являющихся дискретными по своей природе (т.е. счетное число объектов).

Представление в памяти.

Для представления чисел со знаком в ряде компьютеров был использован метод, называемый методом знака и значения. Обычно для знака отводится первый (или самый левый) бит двоичного числа затем следует запись самого числа.

Например, +10 и -15 в двоичном виде можно представить так:

Число	Знаковый бит	Величина
+10	0	0001010
-15	1	0001111

Отметим, что по соглашению 0 используется для представления знака плюс и 1 - для минуса. Такое представление удобно для программистов т.к. легко воспринимается, но не является экономичным.

Если требуется сложить или вычесть два числа, то для решения вопроса о том, какие действия следует при этом предпринять, надо сначала определить знак каждого числа. Например, сложение чисел +6 и -7 на самом деле подразумевает операцию вычитания, а вычитание -6 из +7 операцию сложения. Для анализа знакового бита требуется особая схема и, кроме того, при представлении числа в виде знака и величины необходимы отдельные устройства для сложения и вычитания, т.е., если положительное и отрицательные числа представлены в прямом коде, операции над кодами знаков выполняются раздельно. Поэтому представление чисел в виде знака и значения не нашло широкого применения.

В то же время, при помощи обратного и дополнительного кодов, используемых для представления отрицательных чисел, операция вычитания (алгебраического сложения) сводится к операции простого арифметического сложения. При этом операция сложения распространяется и на разряды знаков, рассматриваемых как разряды целой части числа. Именно поэтому для представления целых чисел со знаком применяется дополнительный код.

Дополнительный код отрицательного числа формируется по следующим правилам:

модуль отрицательного числа записать в прямом коде, в неиспользуемые старшие биты записать нули;
сформировать обратный код числа, для этого нуль заменить единицей, а единицу заменить нулем;
к обратному коду числа прибавить единицу.

Например, для числа -33 в формате integer: 1000000000100001 прямой код 0111111111011110 обратный код +_______________1 1111111111011111 дополнительный код

Для положительных чисел прямой, обратный и дополнительный коды одинаковы. Аналогично представляются целые числа в формате shortint, longint, comp.

При разработке программ на этапе выбора типа данных важно знать диапазон целых величин, которые могут храниться в n разрядах памяти. В соответствии с алгоритмом преобразования двоичных чисел в десятичные, формула суммирования для n разрядов имеет вид:

n-1 2^0 + 2^1 + 2^3 + ... + 2^(n-1), или СУММА (2^i) = 2^n - 1. i=0

При n-битовом хранении числа в дополнительном коде первый бит выражает знак целого числа. Поэтому положительные числа представляются в диапазоне от 0 до 1*2^0 + 1*2^1 +...+ 1*2^(n-2) или от 0 до 2^(n-1) - 1. Все другие конфигурации битов выражают отрицательные числа в диапазоне от -2^(n-1) до -1. Таким образом, можно сказать, что число N может храниться в n разрядах памяти, если его значение находится в диапазоне:

-2^(n-1)

Тип	Диапазон значений	Машинное представление
shortint	-128..127	8 бит, со знаком
integer	-32768..32767	16 бит, со знаком
longint	-2147483648..2147483647	32 бита, со знаком
byte	0..255	8 бит, без знака
word	0..65535	16 бит, без знака
comp	-2^63+1..2^63-1	64 бита, со знаком

Таблица 2.1

Иными словами, диапазон возможных значений целых типов зависит от их внутреннего представления, которое может занимать 1, 2 или 4 байта. В таблице 2.1 приводится перечень целых типов, размер памяти для их внутреннего представления в битах, диапазон возможных значений.

Машинное представление беззнаковых типов.

К беззнаковым типам в PASCAL относятся типы BYTE и WORD.

Формат машинного представления чисел типа BYTE приведен на рис 2.2. а).

Например: 1). Машинное представление числа 45: 45=2^5+2^3+2^2+2^0 = 00101101 2). Машинное представление границ диапазона допустимых значений чисел 0 и 255: 0: 00000000; 255: 11111111.

Рис. 2.2. Формат машинного представления беззнаковых чисел

Формат машинного представления чисел типа WORD приведен на рис. 2.2. б).

Например: 1). Машинное представление числа 258: 257=2^8+2^1 = 00000010 00000001. 2). Машинное представление границ: 0: 00000000 00000000; 65535: 11111111 11111111.

Машинное представление чисел со знаком.

Для представления чисел со знаком определены следующие типы SHORTINT, INTEGER, LONGINT. В приведенных типах числа хранятся в дополнительном ко- де. Напомним, что дополнительный код положительных чисел совпадает с прямым кодом.

Формат машинного представления чисел типа SHORTINT приведен на рис 2.3. а) где s-знаковый разряд числа. Для положительных чисел s=0, для отрицательных s=1.

Например, машинное представление чисел в формате shortint: 1). 0: 00000000; 2). +127: 01111111; 3). -128: 10000000.

Формат машинного представления чисел типа INTEGER приведен на рис 2.3. б). Например:

1). +32765: 11111101 01111111; 2). -32765: 00000011 10000000; 3). -47: 11010001 11111111.

Машинное представление границ диапазона допустимых значений:

4). -32768: 00000000 10000000; 5). 32767: 11111111 01111111.

Формат машинного представления чисел типа LONGINT приведен на рис 2.3. в). Например, представление чисел в формате longint:

1). +89 01011001 00000000 00000000 00000000; 2). -89 10100111 11111111 11111111 11111111.

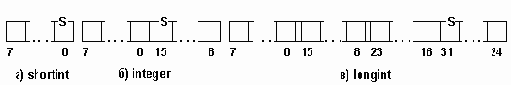
Рис. 2.3. Формат машинного представления чисел со знаком

На рис 2.3 s-знаковый бит числа. При этом, если s=0, то число положительное, если s=1 - число отрицательное. Цифры определяют номера разрядов памяти.

Машинное представление данных типа COMP. . 0 Тип COMP предназначен для работы с большими целыми числами (см. таблицу 2.1). Поэтому числа данного типа представляются в памяти в соответствии с правилами представления целых чисел со знаком - в дополнительном коде. Но для удобства пользователей при вводе и выводе значений чисел в этом формате допускается использование формы записи чисел характерных для вещественных чисел (в виде мантиссы и порядка).

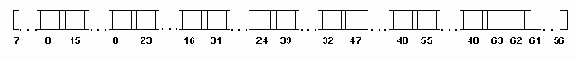
Рис. 2.4. Формат машинного представления данных типа COMP

где s - знаковый разряд числа (если s=0,то число положительное, если s=1 - число отрицательное )

Например: машинное представление чисел в формате COMP: +512 0..0 00000010 0..0 0..0 0..0 0..0 0..0 0..0 -512 0..0 11111110 1..1 1..1 1..1 1..1 1..1 1..1

Содержание раздела