Деревья Хаффмена (деревья минимального кодирования)
Пусть требуется закодировать длинное сообщение в виде строки битов: А В А С С D А кодом, минимизирующим длину закодированного сообщения.
1) назначим коды:
| Символ | Код |
| A | 010 |
| B | 100 |
| C | 000 |
| D | 111 |
А В А С С D А
7*3=21 всего 21 бит - неэффективно
2) Сделаем иначе: предположим, что каждому символу назначен 2-битовый код
| Символ | Код |
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
А В А С С D А
Тогда кодировка требует лишь 14 бит.
3) Выберем коды, которые минимизируют длину сообщения по частоте вхождений символа в строку: много вхождений - код короткий, мало вхождений - код длинный.
А -3 раза, С -2 раза, В -1 раз, D -1 раз то-есть можно:
- 1. использовать коды переменной длины.
- 2. код одного символа не должен совпадать с кодом другого (раскодирование идет слева направо).
Если А имеет код 0 т.к часто встречается, то В, С, D - начинаются с 1, если дальше 0,то это С, следующий может быть 0 или 1: 1 - D , 0 - В; то-есть В и D различаются по последнему биту, А -по первому, С - по второму, B и D - по третьему.
| Символ | Код |
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
Таким образом, если известны частоты появления символов в сообщении, то метод реализует оптимальную схему кодирования.
Частота появления группы символов равна сумме частот появления каждого символа.
Сообщение АВАССDА кодируется как 0110010101110 и требует лишь 13 бит.
В очень длинных сообщениях, которые содержат символы, встречающиеся очень редко - экономия существенна.
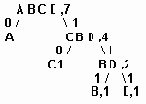
Рис.6.30 Дерево Хаффмена
Обычно коды создаются на основе частоты во всем множестве сообщений, а не только в одном.
