Логическая структура, определения
Граф - это сложная нелинейная многосвязная динамическая структура, отображающая свойства и связи сложного объекта.
Многосвязная структура обладает следующими свойствами:
- 1) на каждый элемент (узел, вершину) может быть произвольное количество ссылок;
- 2) каждый элемент может иметь связь с любым количеством других элементов;
- 3) каждая связка (ребро, дуга) может иметь направление и вес.
В узлах графа содержится информация об элементах объекта. Связи между узлами задаются ребрами графа. Ребра графа могут иметь направленность, показываемую стрелками, тогда они называются ориентированными, ребра без стрелок - неориентированные.
Граф, все связи которого ориентированные, называется ориентированным графом или орграфом; граф со всеми неориентированными связями - неориентированным графом; граф со связями обоих типов - смешанным графом. Обозначение связей: неориентированных - (A,B), ориентированных - . Примеры изображений графов даны на рис.6.1. Скобочное представление графов рис.6.1:
а).((A,B),(B,A)) и б).(< A,B >,< B,A >).
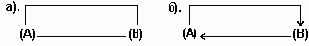
Рис.6.1. Граф неориентированный (а) и ориентированный (б).
Для ориентированного графа число ребер, входящих в узел, называется полустепенью захода узла, выходящих из узела -полустепенью исхода. Количество входящих и выходящих ребер может быть любым, в том числе и нулевым. Граф без ребер является нуль-графом.
Если ребрам графа соответствуют некоторые значения, то граф и ребра называются взвешенными. Мультиграфом называется граф, имеющий параллельные (соединяющие одни и те же вершины) ребра, в противном случае граф называется простым.
Путь в графе - это последовательность узлов, связанных ребрами; элементарным называется путь, в котором все ребра различны, простым называется путь, в котором все вершины различны. Путь от узла к самому себе называется циклом, а граф, содержащий такие пути - циклическим.
Два узла графа смежны, если существует путь от одного из них до другого. Узел называется инцидентным к ребру, если он является его вершиной, т.е.
ребро направлено к этому узлу.
Логически структура- граф может быть представлена матрицей смежности или матрицей инцидентности.
Матрицей смежности для n узлов называется квадратная матрица adj порядка n. Элемент матрицы a(i,j) равен 1, если узел j смежен с узлом i (есть путь < i,j >), и 0 -в противном случае (рис.6.2).
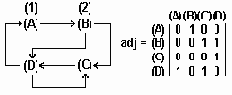
Рис.6.2. Графа и его матрица смежности
Если граф неориентирован, то a(i,j)=a(j,i), т.е. матрица симметрична относительно главной диагонали.
Матрицы смежности используются при построении матриц путей, дающих представление о графе по длине пути: путь длиной в 1 - смежный участок - , путь длиной 2 - (< A,B >,< B,C >), ... в n смежных участков: где n - максимальная длина, равная числу узлов графа. На рис.6.3 даны путевые матирцы пути adj2, adj3, adj4 для графа рис.6.2.
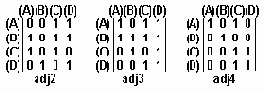
Рис.6.3. Матрицы путей
Матрицы инцидентности используются только для орграфов. В каждой строке содержится упорядоченная последовательность имен узлов, с которыми данный узел связан ориетрированными (исходящими) ребрами. На рис.6.4 показана матрица инцидентности для графа рис. 6.2.
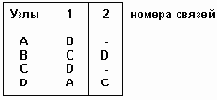
Рис.6.4. Матрицы инцидентности
