Вещественные типы
В отличии от порядковых типов (все целые, символьный, логический), значения которых всегда сопоставляются с рядом целых чисел и, следовательно, представляются в памяти машины абсолютно точно, значение вещественных типов определяет число лишь с некоторой конечной точностью, зависящей от внутреннего формата вещественного числа.
Представление вещественных чисел в памяти.
В некоторых областях вычислений требуются очень большие или весьма малые действительные числа. Для получения большей точности применяют запись чисел с плавающей точкой. Запись числа в формате с плавающей точкой является весьма эффективным средством представления очень больших и весьма малых вещественных чисел при условии, что они содержат ограниченное число значащих цифр, и, следовательно, не все вещественные числа могут быть представлены в памяти. Обычно число используемых при вычислениях значащих цифр таково, что для большинства задач ошибки округления пренебрежимо малы.
Формат для представления чисел с плавающей точкой содержит одно или два поля фиксированной длины для знаков. Количество позиций для значащих цифр различно в разных ЭВМ, но существует, тем не менее, общий формат, приведенный на рисунке 2.5 а). В соответствии с этой записью формат вещественного числа содержит в общем случае поля мантиссы, порядка и знаков мантиссы и порядка.

Рис. 2.5. Формат представления вещественных чисел
Однако, чаще вместо порядка используется характеристика, получающаяся прибавлением к порядку такого смещения, чтобы характеристика была всегда положительный. При этом имеет место формат представления вещественных чисел такой, как на рис 2.5 б).
Введение характеристики избавляет от необходимости выделять один бит для знака порядка и упрощает выполнение операций сравнения (,=) и арифметических операций над вещественными числами. Так, при сложении или вычитании чисел с плавающей точкой для того, чтобы выровнять операнды, требуется сдвиг влево или вправо мантиссы числа. Сдвиг можно осуществить с помощью единственного счетчика, в который сначала заносится положительное чис- ло, уменьшающееся затем до тех пор, пока не будет выполнено требуемое число сдвигов.
Таким образом, для представления вещественных чисел в памяти ЭВМ порядок p вещественного числа представляется в виде характеристики путем добавления смещения (старшего бита порядка):
Х = 2^(n-1) + k + p, (2.1)
где:
- n - число бит, отведенных для характеристики,
- p - порядок числа,
- k - поправочный коэффициент фирмы IBM, равный +1 для real
- и -1 для форматов single, double, extended.
Формулы для вычисления характеристики и количество бит, необходимых для ее хранения, приведены в таблице 2.2.
| Тип | Харрактеристика | Кол-во бит на хар-ку |
| real | x = 2^7 + p + 1 | 8 |
| single | x = 2^7 + p - 1 | 8 |
| double | x = 2^10 + p - 1 | 11 |
| extended | x = 2^14 + p - 1 | 15 |
Следующим компонентом представляемого в машине числа с плавающей точкой является мантисса. Для увеличения количества значащих цифр в представлении числа и исключения переполнения при умножении мантиссу обычно подвергают нормализации. Нормализация означает, что мантисса (назовем ее F), кроме случая, когда F=0, должна находиться в интервале
R^(-1)
Для двоичной системы счисления R=2. Тогда в связи с тем, что 2^(-1)
Приведенный метод нормализации является классическим методом, при котором результат нормализации представляется в виде правильной дроби, т.е. с единицей после точки и нулем в целой части числа. Но нормализацию мантиссы можно выполнить по разному.
В IBM PC нормализованная мантисса содержит свой старший бит слева от точки. Иными словами нормализованная мантисса в IBM PC принадлежит интервалу 1
Первый, старший, бит в представлении чисел в формате с плавающей точкой является знаковым, и по принятому соглашению нуль обозначает положительное число, а единица - отрицательное.
Число бит для хранения мантиссы и порядка зависит от типа вещественного числа. Суммарное количество байтов, диапазоны допустимых значений чисел вещественных типов, а также количество значащих цифр после запятой в представлении чисел приведены в таблице 2.3.
| Тип | Диапазон значений | Значащие цифры | Размер в байтах |
| real | 2.9*10^(-39)..1.7*10^38 | 11-12 | 6 |
| single | 1.4*10^(-45)..3.4*10^38 | 7-8 | 4 |
| double | 4.9*10^(-324)..1.8*10^308 | 15-16 | 8 |
| extended | 3.1*10^(-4944)..1.2*10^4932 | 19-20 | 10 |
Таблица 2.3
Алгоритм формирования машинного представления вещественного числа в памяти ЭВМ
Алгоритм формирования состоит из следующих пунктов:
- 1). Число представляется в двоичном коде.
- 2). Двоичное число нормализуется. При этом для чисел, больших единицы, плавающая точка переносится влево, определяя положительный порядок. Для чисел, меньших единицы, точка переносится вправо, определяя отрицательный порядок.
- 3). По формуле из таблицы 2.2 с учетом типа вещественного числа определяется характеристика.
- 4). В отведенное в памяти поле в соответствии с типом числа записываются мантисса, характеристика и знак числа. При этом необходимо отметить следующее:
- - для чисел типа real характеристика хранится в младшем байте памяти, для чисел типа single, double, extended - в старших байтах;
- - знак числа находится всегда в старшем бите старшего байта;
- - мантисса всегда хранится в прямом коде;
- - целая часть мантиссы (для нормализованного числа всегда 1) для чисел типа real, single, double не хранится (является скрытой). В числах типа extended все разряды мантиссы хранятся в памяти ЭВМ.
Машинное представление данных типа REAL Формат машинного представления данных типа REAL следующий:
мл. байт ст. байт а: 7 0 15 8 23 16 31 24 39 32 47 40 x....x м....м м....м м....м м....м sм...м б: 7 0 -32 -39 -24 -31 -16 -23 -8 -15 -1 -7
где:
- а - номера разрядов памяти,
- б - показатели степеней разрядов характеристики и мантиссы,
- s - знаковый разряд числа,
- м - нормализованная мантисса,
- х - характеристика числа.
Например:
1). Десятичное число 15.375;
в двоичной системе счисления 1111.011; результат нормализации 1.111011*2^3; р=3.
Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: s=0; х=2^7+1+3=2^7+2^2=132;
в двоичной системе счисления х=10000100; м=1110110...0;
машинное представление числа: 10000100 00000000 00000000 00000000 00000000 01110110
2). Десятичное число -0.5;
аналогичные выкладки дают: нормализованную мантиссу: 1.00...0;
машинное представление числа: 10000000 00000000 00000000 00000000 00000000 10000000
3). Десятичное число -25.75;
аналогично: нормализованная мантисса: 1.10011100...0;
машинное представление числа: 10000101 00000000 00000000 00000000 00000000 11001110
4). Число 0.0;
Машинное представление числа: 00000000 00000000 00000000 00000000 00000000 00000000
5). Числа верхней и нижней границ положительного диапазона
~1.7*10^38 - 11111111 11111111 11111111 11111111 11111111 01111111 ~2.9*10^(-35) - 00000001 00000000 00000000 00000000 00000000 00000000
Машинное представление данных типа SINGLE
Формат машинного представления данных типа SINGLE следующий:
мл. байт ст. байт 7 0 15 8 23 22 16 31 30 24 - номера разрядов памяти м....м м....м х м...м s х...х -16 -23 -8 -15 0 -1 -7 7 1 - показатели степеней разрядов мантиссы и характеристики
где:
- s - знаковый разряд,
- х - характеристика числа,
- м - нормализованная мантисса.
Например:
1). Число -15.375;
в двоичной системе счисления -1111.011; нормализованное двоичное число -1.111011*2^3; р=3.
Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: s=1; х=2^7-1+3=2^7+2^1=130;
в двоичной системе счисления х=10000010; м=1110110...0;
машинное представление числа в формате SINGLE:
00000000 00000000 01110110 11000001
2). Число -0.1875;
в двоичной системе счисления -0.0011; нормализованное двоичное число -1.1*2^(-3); р=-3.
Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: s=1; х=2^7-1-3=2^7-2^2;
в двоичной системе счисления х=01111100; м=100...0;
машинное представление числа в формате SINGLE:
00000000 00000000 01000000 10111110
3). Десятичное число 4.5;
аналогичные выкладки дают нормализованную мантиссу: 1.00100...0;
машинное представление числа: 00000000 00000000 10010000 01000000
4). Значения верхней и нижней границ чисел отрицательного диапазона
~-3.4*10^38 - 11111111 11111111 01111111 11111111 ~-.4*10^(-45) - 00000001 00000000 00000000 10000000
Машинное представление данных типа DOUBLE
Формат машинного представления данных типа DOUBLE следующий:
мл.байт ст.байт 7 0 15 8 23 16 31 24 39 32 47 40 55 52 51 48 63 56 м...м м...м м...м м...м м...м м...м х..х м...м s x..x -44 -50 -37 -43 -29 -36 -21 -28 -13 -20 -5 -12 3 0 -1 -4 10 4
где:
- верхняя строка цифр от 0 до 63 - номера разрядов памяти;
- нижняя строка цифр от -50 до -1 - показатели степеней разрядов мантиссы; от 0 до 10 - разрядов характеристики;
- s - знаковый разряд числа;
- м - нормализованная мантисса;
- х - характеристика числа (x=2^10-1+p, где p - порядок нормализованного числа).
Например:
1). Число 15.375;
в двоичной системе счисления 1111.011; результат нормализации 1.111011*2^3; р=3.
Учитывая отбрасывание скрытой единицы и сдвиг порядка, получаем: s=0; x=2^10-1+3=2^10+2^1=1026;
в двоичной системе счисления х=10000000010; m=1110110...0;
машинное представление числа в формате DOUBLE:
0 00000000 00000000 00000000 00000000 31 32 00000000 11000000 00101110 01000000 63
2). Десятичное число 0.0375;
в двоичной системе счисления 0.011; результат нормализации 1.1*2^(-2); р=-2.
Учитывая отбрасывание скрытой единицы и сдвиг порядка, получаем: s=0; x=2^10-2^1-2^0=2^10-3;
в двоичной системе счисления х=01111111101; m=100...0;
машинное представление числа в формате DOUBLE:
0 00000000 00000000 00000000 00000000 31 32 00000000 00000000 11011000 00111111 63
3). Десятичное число 2.5;
аналогичные выкладки дают нормализованную мантиссу: 1.0100...0;
машинное представление числа 2.5: 00000000 00000000 00000000 00000000 00000000 00000000 00000100 01000000
4). Значения верхней и нижней границ диапазона положительных чисел:
~1.8*10^308 - 11111111 11111111 11111111 11111111 11111111 11111111 11101111 01111111 ~4.9*10^(-324) - 00000001 00000000 00000000 00000000 00000000 00000000 00000000 00000000
Символ ~ обозначает приближенное значение числа.
Машинное представление данных типа EXTENDED
Формат машинного представления данных типа EXTENDED следующий:
мл.байт ст. байт 7 0 15 8 23 16 31 24 39 32 47 40 55 48 63 56 71 64 79 72 м..м м..м м..м м..м м..м м..м м..м м..м х..х sх..х -56-63-48-55-40-47-32-39-24-31-16-23-8 -15 0 -7 7 0 14 8
где:
- верхняя строка цифр - номера разрядов памяти;
- нижняя строка цифр - показатели степеней разрядов мантиссы и характеристики;
- s - знаковый разряд числа;
- м - нормализованная мантисса;
- х - характеристика числа.
Например:
1). Число -15.375;
в двоичной системе счисления -1111.011; после нормализации -1.111011*2^3; р=3.
Учитывая присутствие скрытой единицы и сдвиг порядка, получаем: s=1; х=2^14-1+3=2^14+2^1=16386;
в двоичной системе счисления х=100000000000010; м=11110110...0
( в мантиссе единица стоящая слева от запятой не отбрасывается).
Машинное представление данного числа в формате EXTENDED:
0..0 0..0 0..0 0..0 0..0 0..0 0..0 11110110 00000010 11000000
2). Число 1.0;
аналогичные выкладки дают нормализованную мантиссу: 1.0...0; машинное представление числа 1.0: 0..0 0..0 0..0 0..0 0..0 0..0 0..0 10000000 11111111 00111111
3). Значения верхней и нижней границ диапазона положительных чисел
(символом * помечены разряды, значения которых при данной характеристике не идентифицируются т. е. их значения не влияют на значение мантиссы):
~1.2*10^4932 - ******** ******** 11111111 11111111 11111111 11111111 11111111 11111111 11111111 011111111 ~3.1*10^4944 - ******** ******** 00000001 00000000 000000000 00000000 00000000 00000000 00000001 000000000
2.1.3. Десятичные типы
Десятичные типы не поддерживаются языком PASCAL, но имеются в некоторых других языках, например, COBOL, PL/1. Эти типы приме няются для внутримашинного представления таких данных, которые в первую очередь должны храниться в вычислительной системе и выдаваться пользователю по требованию, и лишь во вторую очередь - обрабатываться (служить операндами вычислительных операций). Неслучайно эти типы впервые появились в языке COBOL, ориентированном на обработку экономической информации: в большинстве задач этой сферы важно прежде всего хранить и находить информацию, а ее преобразование выполняется сравнительно редко и сводится к простейшим арифметическим операциям.
Архитектура некоторых вычислительных систем (например, IBM System/390) предусматривает команды, работающие с десятичным представлением чисел, хотя эти команды и выполняются гораздо медленнее, чем команды двоичной арифметики. В других архитектурах операции с десятичными числами моделируются программно.
К десятичным типам относятся: десятичный тип с фиксированной точкой и тип шаблона.
Десятичный тип с фиксированной точкой.
В языке PL/1 десятичный тип с фиксированной точкой описывается в программе, как:
DECIMAL FIXED (m.d) или DECIMAL FIXED (m).
Первое описание означает, что данное представляется в виде числа, состоящего из m десятичных цифр, из которых d цифр расположены после десятичной точки. Второе - целое число из m десятичных цифр. Следует подчеркнуть, что в любом случае число десятичных цифр в числе фиксировано. Внутримашинное представление целых чисел и чисел с дробной частью одинаково. Для последних положение десятичной точки запоминается компилятором и учитывается им при трансляции операций, в которых участвуют десятичные числа с фиксированной точкой.
Внутримашинное представление данного типа носит название десятичного упакованного формата. Примеры представления чисел в таком формате приведены на рис. 2.6.
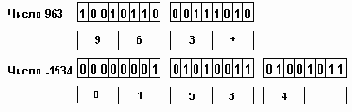
Рис.2.6. Машинное представление десятичных чисел в упакованном формате
Каждая десятичная цифра числа занимает полбайта (4 двоичных разряда) и представляется в этом полубайте ее двоичным кодом. Еще полбайта занимает знак числа, который представляется двоичным кодом 1010 - знак "+" или 1011 - знак "-". Представление занимает целое число байт и при необходимости дополняется ведущим нулем.
Тип шаблона.
В языке PL/1 тип шаблона описывается в программе, как: PICTURE '9...9'.
Это означает, что данное представляет собой целое число, содержащее столько цифр, сколько девяток указано в описании.
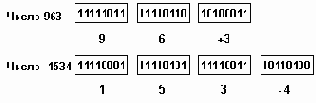
Рис.2.7. Машинное представление десятичных чисел в зонном формате
Внутримашинное представление этого типа, так называемый десятичный зонный формат, весьма близок к такому представлению данных, которое удобно пользователю: каждая десятичная цифра представляется байтом: содержащим код символа соответствующей цифры. В IBM System/390, которая аппаратно поддерживает зонный формат, применяется символьный код EBCDIC, в котором код символа цифры содержит в старшем полубайте код 1111, а в младшем - двоичный код цифры числа.Знак не входит в общее число цифр в числе, для представления знака в старшем полубайте последней цифры числа код 1111 заменяется на 1010 - знак "+" или 1011 - знак "-".
Примеры представления чисел в зонном формате приведены на рис.2.7.
